Gilbert Vidal, Le Chesnay-Rocquencourt (France)
2nd edition, March 31, 2025
This edition cancels and replaces that of December 10, 2024. The main modifications concern C3 and C2a.
INTRODUCTION
Dear readers, below is a five-point demonstration (D1 to D5) that, in the context of Euclidean geometry, the Moon does not rotate on itself. It includes and bases on a second demonstration: the point D4, purely mathematical and irrefutable.
Astronomers and mathematicians assert on the contrary that the Moon spins. However they also agree that the matter should be analyzed according to the axioms and theorems of Euclidean geometry. This incoherence brings us to an intriguing situation: a glaring, old and universally accepted error is still existing in a formal science. Given its uniqueness, I will refer to this as the Error.
I argue that correcting the Error is not fundamentally an issue of astronomy or mathematics, but rather a problem of collective psychology. My stance is grounded in approximately thirteen years of exchanges with scientists. Persistently, I have submitted the D4 demonstration, in various forms, via email. The few who have replied (whom I gratefully acknowledge) typically disregarded it, and some outright contested it. My attempts in forums have been equally fruitless. As for organizations, such as NASA or the French National Education or the French Academy of Sciences, they did not answer me. The “Psychological side” chapter will attempt to shed light on these reactions.
When scientists have unequivocally approved the D4 demonstration, the three pillars of Error will quickly collapse. These are:
a) the Distant Star Convention denounced in C2
b) the synchronous rotation denounced in C10a
c) the rotation of distant stars denounced in C10b.
Then can we reap the fruits of Error. It will indeed offer valuable insights for epistemologists, psychologists, and philosophers into how such deep-seated misconceptions could dominate even the greatest minds for so long.
My objective is to acquire public recognition from a scientific institution (such as an observatory or a university) of the fact that the Moon does not spin, that is non-spinning Moon. Which one will it be?
PRELIMINARIES
We will admit that the expression “rotates on itself” is equivalent to “rotates around its axis”, or “spins”; that the axis of the Moon is unique, passes through its center and is perpendicular to the orbital plane; that there are no alternative rotations like librations.
The acronym SM (Spinning Moon) designates the concept which assumes that the Moon rotates on its axis. The acronym NSM (Non-Spinning Moon) denotes the opposite design.
In the SM the Moon is subject to two rotations, the first around the Earth and the second around its axis. In the NSM the Moon is subject to only one rotation, the first one.
The acronym EG (Euclidean Geometry) designates any geometry built on the five axioms of Euclid.
DEMONSTRATION OF THE NSM
D1/ Henri Poincaré could tell us that the choice between NSM and SM depends on the set of conventions that we have set for ourselves. This set necessarily includes the axioms of a geometry, in order to make space accessible to mathematical reasoning.
D2/ Given its preeminence in the solar system, the EG is essential to make the choice between NSM and SM. Our set of conventions therefore includes (at least) Euclid’s five axioms.
D3/ The universal model
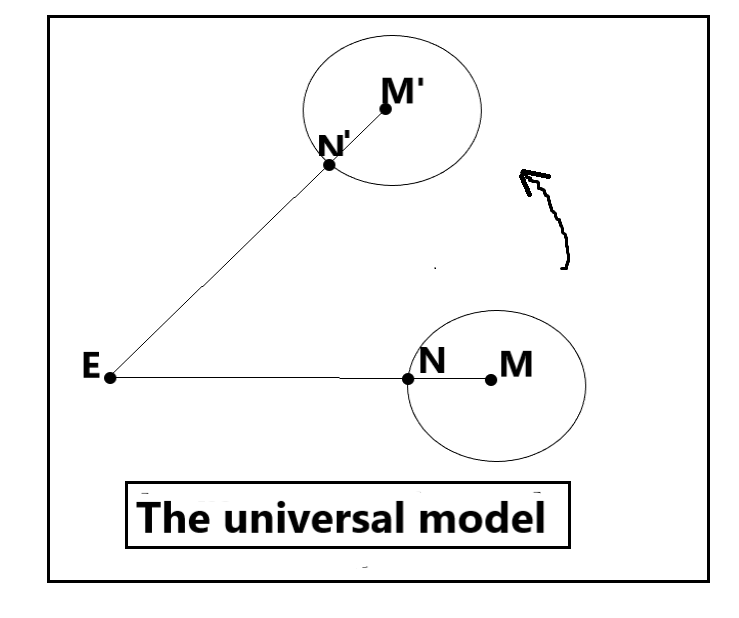
In the plan, the mathematical disk with center M (Moon) representing the Moon rotates around point E (Earth) representing the center of the Earth. Point N (Nearest) represents the Moon’s point closest to Earth, of sélénographic coordinates (0,0). These three points always remain aligned when the disk rotates around point E.
Note: An emblematic figure of the universal model is that of the left of the NASA site: https://science.nasa.gov/moon/tidal-locking/. We can place the points E, N and M there by thought, then note their permanent alignment.
D4/ Mathematical demonstration of the NSD (Non-Spinning Disk)
Let us first consider the movement of the line segment MN alone, removing the disk by thought. This segment simply rotates around point E. It cannot rotate around point M because a second rotation around the latter could only break the alignment of points E, N and M.
Note 1: Moreover, the segment MN is unaware for the moment that the point M will be promoted to “center-of-disc”. Why would it rotate around M rather than around N or the middle of MN, or any other of its points?
Now consider the model in its entirety. The points M and N being both linked to the disk, the latter behaves like the segment MN. We conclude that the disk does not rotate around point M.
Note 2: The above demonstration could have been made by Euclid. Nowadays it can be reduced to the following: We go from the disk with center M to the disk with center M’ by one and only one rotation with center E and angle MEM’.
D5/ The Moon therefore does not rotate on its axis.
COMMENTS
C1/ In a coherent set of axioms and propositions, any demonstrated proposition cannot be invalidated elsewhere inside this set.
C2/ The Distant Star Convention (DSC)
When it comes to the rotation of stars, astronomers rely on the following convention: “when we say that a planet rotates on itself it is relative to a fixed direction provided by a distant star”. However, it cannot be added to Euclid’s five axioms for the reason given in C1. Indeed, it would allow to contradict what was demonstrated in D4 within the EG. Its use would require a new geometry which doesn’t exist. If this convention is due to Mach’s principle, then we must reject the application of this principle in the solar system due to incompatibility with the EG and absence of a substitute geometry.
C2a/ As DSC is the main cause of the notion of sidereal rotation, the sidereal rotations of all the stars of the solar system must be considered fictitious; only synodic rotations are real. The Earth completes one real revolution in 24 hours and not 24 minus 4 minutes; Mercury is in a 1:2 spin-orbit resonance with the Sun (1 spin for 2 orbits) and not 3:2; etc…
C3/ This comment, which appeared in the December 10, 2024 edition, was uncalled for. It was both off-topic and false. I beg your pardon, dear readers.
C4/ Certainly all celestial bodies rotate. But that doesn’t mean they all turn on themselves.
C5/ Certainly the EG must give way to other geometries if we want to account for General Relativity. But, in the solar system, the resulting corrections would be far too small to change an NSM into an SM.
C6/ The native EG founds all the classical sciences of space which will appear after Euclid, namely: analytical geometry which links the EG to algebra (17 centuries later), then kinematics which introduces time, then classical mechanics that defines and introduces strength. Euclid’s five axioms are the guarantors of the coherence of this vast whole.
C7/ We deduce from C1 and C6 that, the NSM being demonstrated in the EG, no theory or no experiment can claim to invalidate it, whatever their notoriety. The only way to do this would be to change geometry.
C8/ The model
By definition, the object behaves like the model that represents it; this is why, in the demonstration of the NSM, D5 is the direct consequence of D4.
The choice between NSM and SM can only be made by reasoning on a model. In the event of a disagreement between reality and the model, it is the first which takes precedence, but we must then find another model conforming both to reality and the conventions that we have set for ourselves, or else change the latter.
C8a/ There is no model of SM that could satisfy both observation (the three aligned points) and EG.
C9/ The universal model
All known models that deal with our subject come down to the universal model presented in the demonstration. We can place the 3 points E, N and M on each of them, then note their permanent alignment.
The universal model is correct; I only contest its interpretation.
It represents in a simplified manner the Moon observed from the celestial north in a reference system preferably geocentric, knowing that the heliocentric or the galactic would lead to the same result because the influences of the Sun on the Earth or of the Galaxy on the Sun are too weak to change the NSM to SM.
We can besides generalize it to any form of figure or trajectory because the angle of rotation MEM’ can be chosen as small as we want; we deduce the following theorem: “In Euclidean plane geometry, if a figure moves while keeping two of its points aligned with a third fixed point, whatever its shape and whatever its trajectory, then this figure does not rotate on itself.”
C9a/ The right part of the video of the NASA site noted in D3 shows a disk which rotates in the opposite direction of the orbit. Scientists wrongly interpret both left and right parts of the video by applying the DSC instead of the EG.
C10/ In additon to the DSC cited in C2, I have noticed that my correspondents essentially rely on two other prejudices: the synchronous rotation and the rotation of the stars
C10a/ Synchronous rotation (SR)
SR is only a consequence of SM, so it cannot exist if SM doesn’t. Incomprehensibly, despite its subordinate status, it has taken on such importance that it is presented as the main proof of the existence of SM. Scientists thus claim to prove A ( SM exists) by B ( SR exists) while B presupposes A, which is a serious mistake in logic called circular reasoning.
ChatGPT allows us to realize the place taken by SR in its data base, as shown by the two following examples:
It unequivocally recognizes that a geostationary satellite behaves geometrically like the Moon. It also recognizes that the first does not rotate on itself. But it stubbornly refuses to do the same for the Moon, invoking the SR.
By directly introducing the five points D1 to D5 of the demonstration into ChatGPT, I could see that it often approves the first four. But it always rejects D5 by invoking both SR and the rotation of distant stars (at least for the moment, because progress in AI is dazzling).
Note: ChatGPT responses are known to vary from one regeneration to another. The best thing is to try it yourself.
C10b/ The rotation of distant stars
SM is often justified by the fact that an astronaut on the Moon sees the stars rotating. This is a big mistake. There is no need for the Moon to rotate on itself to obtain this effect; the revolution around the Earth is sufficient.
This error appears in different forms in mental experiments like that of the two waltzers or the similar one of the late Hubert Reeves in his video on the site https://www.youtube.com/watch?v=RODh1gte1lU. The masterful divulgator presents two characters rotating with outstretched arms while holding each other’s hands. From the mere fact that they see their environment rotating, he concludes that they are rotating on themselves. It is easy to contradict, for example using classical mechanics, which prohibits an undeformable body from rotating around three parallel axes.
C11/ We can find many other false justifications for SM, on the Internet and in my email box. They are based on (false) interpretations of a host of models or mental experiments (most often correct) which ignore any scientific tool; these are reasonings which take us back to the pre-Euclidean era, with the resulting errors.
The most disturbing mental experiment involves bringing the Moon closer to Earth. The Moon then seems to rotate more and more on itself. In a first phase, as long as the centers are separated, the experience remains valid (but its interpretation remains as false); it is simply a reinforcement of the optical illusion. In a second phase, a subtle transition to the limit occurs: when the centers merge, we could actually say that the Moon rotates on itself. Unfortunately, the orbit disappeared at the last moment, and with it the validity of the experiment.
Some amateurs defend the NSM in forums on the Internet, but with always pre-Euclidean reasonings.
C12/ If a gyroscope of sufficient resolution is one day installed on the Moon’s equator, it will not detect any radial acceleration due to any continuous rotation of the Moon on itself; it will only detect that due to its revolution. This experience will force us to abandon SM. Why wait for such a predictable event to react?
Note: The longitudinal libration of an NSM can be explained by the classical mechanics. I propose a rough simulation in Python of it in a dedicated page of this site.
PSYCHOLOGICAL SIDE
The stubborn rejection of scientists is explained firstly by my own situation: as a simple engineer, unknown and isolated moreover (I am by nature not very communicative, and the little social life I had evaporated since I retired), I find myself deprived of access to scientific journals and have been unable to obtain any support; I was never able to get an interview which would have helped considerably. However, overall, I consider myself lucky to have benefited from the kindness of correspondents who took the time to respond to a more or less conspiratorial stranger. I understand their reluctance.
However, I understood less why the purely mathematical part of my demonstration was ignored, or even refuted. How could superior minds make mistakes that would make a high school student blush?
I only discovered it recently when reading Marc Romainville’s book “À l’école du doute” which deals with conspiracy theories and fake news. The author shows us how any argument brought against an idea firmly implanted in people’s minds remains powerless to change them one iota. It is based on Kahneman’s theory according to which, beyond a certain degree of certainty, we remain stuck in what he calls system 1, which uses our reflexes, our instinct, our emotions, etc. We are then blind and deaf to any questioning of our knowledge. Our opponents can only progress by implementing a means likely to activate our system 2, which calls for calm reflection, rigor in reasoning, etc. Undertaking this task is particularly challenging within the realm of formal sciences.
I will present two examples taken from my experience to make you, dear readers, better aware of the path that remains to be accomplished.
The first example concerns a debate that I launched in June 2022 on the “Les-mathématiques.net” forum under the title “Rotation d’un disque”. I was firmly resolved to stay on the mathematical level in order to obtain the support of a mathematician for the demonstration D4, because the only one who had recognized it in previous years did not want to sponsor me. Bingo, a certain Ludwig grants it to me without reservation and even goes so far as to defend it to others. In euphoria I then evoke the Moon. Alas, Ludwig ruins my hopes with a single post in which he reiterates his faith in demonstration, but only after having “demonstrated” SM with a glass rotating on a table around another glass, “…the movement of your hand should help you understand what is happening”. His reaction reflects that of the majority of my French or foreign correspondents. Each person depends on their favored mental experience. Ludwig favors relying on the sensations in his hand over the EG.
The second example concerns a too hasty exchange with a luminary in astrophysics, in October 2023. Barely a quarter of an hour after my sending in which I presented the substance of the demonstration, I received the following email: “Of course the Moon rotates around itself with the same period as its rotation around the Earth. It’s just a combination of movements. To help you see it, isolate the Moon, and you see that the MN vector is rotating”. I then added note 1 in the demonstration.